Be a 2D shape detective
Shapes are all around us. But how much do you know about them?
Be a shape detective and find out more about 2D shapes.
-
Key Stage
-
Art term
-
Created by
-
Topics
© the artist's estate. Image credit: St George's Hospital
About this resource
How many sides does a hexagon have? What is the strongest shape? Where can we see shapes around us?
This resource provides an introduction to common 2D shapes and their properties using artworks.
Through whole class discussion and activities students will:
- learn to recognise and describe common shapes
- find out about the properties of 2D shapes
- explore and discuss where we can see shapes around us in everyday life
- use shapes to make an artwork
This Maths and Art and Design resource offers a series of teacher-led, whole class or group activities. The questions and discussion suggestions are voiced directly to students, allowing the resource to be easily presented to the class. Teachers' guidance notes are included as well as activity ideas for exploring shapes.
The resource can be used together as a lesson plan or as individual components to integrate into your own scheme of work. It is designed for CfE Level 1 / KS 1 students / National Curriculum Wales Foundation Phase Yrs 1 & 2, but can also be adapted for younger age groups.
Curriculum links
National Curriculum for England
Mathematics: Geometry - Properties of shapes
Year 1: Pupils should be taught to recognise and name common shapes, including:
- 2-D shapes [for example, rectangles (including squares), circles and triangles]
Year 2: Pupils should be taught to:
- identify and describe the properties of 2-D shapes, including the number of sides and line symmetry in a vertical line
- compare and sort common 2-D shapes and everyday objects
Northern Ireland Curriculum
Mathematics and Numeracy: Shape and space
Pupils should be enabled to:
- sort 2-D shapes in different ways;
- make constructions, pictures and patterns using 2-D shapes;
- name and describe 2-D shapes;
- recognise reflective symmetry;
- explore simple tessellation through practical activities
Art & design
- use a range of processes
Scotland's Curriculum for Excellence
Numeracy and mathematics
- I have explored simple 2D shapes and can identify, name and describe their features using appropriate vocabulary (MTH 1-16a)
- I can explore and discuss how and why different shapes fit together and create a tiling pattern with them (MTH 1-16b)
Art and design
- I have the opportunity to choose and explore a range of media and technologies to create images and objects, discovering their effects and suitability for specific tasks (EXA 1-02a)
- I can create and present work using the visual elements of line, shape, form, colour, tone, pattern and texture (EXA 1-03a)
National Curriculum for Wales (2008)
Mathematics: Shapes
Year 1
- recognise and name common 2D shapes (square, triangle, rectangle, circle and semi-circle) in order to begin to compare and sort them
Year 2
- recognise and name regular and irregular 2D shapes, understand and use the properties of shape
National Curriculum for Wales (2022)
Mathematics
Geometry focuses on relationships involving shape, space and position, and measurement focuses on quantifying phenomena in the physical world.
Progression step 2:
– I have explored two-dimensional and three-dimensional shapes and their properties in a range of contexts.
– I have explored reflective symmetry in a range of contexts and I can discuss it as a property of shapes and images.
– I have explored the concept of rotation and I am beginning to use simple fractions of a complete rotation to describe turns.
Expessive Arts
Exploring the expressive arts is essential to developing artistic skills and knowledge and it enables learners to become curious and creative individuals.
Progression step 2:
– I can explore how and why creative work is made by asking questions and developing my own answers.
Responding and reflecting, both as artist and audience, is a fundamental part of learning in the expressive arts.
Progression step 2:
– I can give and accept feedback as both artist and audience.
Creating combines skills and knowledge, drawing on the senses, inspiration and imagination.
Progression step 2:
– I am beginning to apply techniques in my creative work with guidance and direction.
– I am beginning to demonstrate resilience and flexibility in approaching creative challenges.
– I can use creative materials safely and with some control under supervision.
© estate of Richard Allen. Image credit: Jersey Heritage
Squares and rectangles
Look at this picture. It is a painting of some shapes. Can you spot a square?
- What colour is the square?
- How many sides does a square have?
- Are all its sides the same length?
- How many corners does it have?
Look at the yellow shape. It looks a bit like a stretched square!
This shape is called a rectangle.
- How is a rectangle similar to a square?
- How is a rectangle different from a square?
- Can you see any more rectangles in the painting?
Did you know? If you cut a square in half you get two rectangles.
About squares and rectangles
A square has 4 corners and 4 straight sides. The sides of a square are all the same length.
A rectangle is similar to a square. It also has 4 corners and 4 straight sides. But the sides of a rectangle are not all the same length. A rectangle has 2 long sides and 2 short sides. The sides of a rectangle that are opposite each other are always the same length.
Teacher notes
Point out to students that rectangles can be of different dimensions – as the rectangles in the painting illustrate.
You could demonstrate folding or cutting a paper square in half to show how this makes two rectangles.
You could also show students how, if you fold or cut a square diagonally you get two triangles... to lead into the next section of this resource!
Triangles
Here is another painting made from shapes. What shapes can you see?
The painting is made of lots of brightly coloured triangles (and bits of triangles). Can you see a yellow triangle? Can you see a green triangle?
Try drawing a triangle in the air with your finger.
- How many sides does a triangle have?
- How many corners does it have?
Not all triangles look the same. Some triangles have sides that are all the same length, others have sides that are different lengths.
Triangle questions...
- Can you find a triangle that has sides the same length?
- Can you find a triangle that has sides that are different lengths?
About triangles
Triangles have 3 corners and 3 sides.
Some triangles have sides that are equal in length. These are called equilateral triangles.
Some triangles have 2 sides of the same length and one side that is a different length. These are called isosceles triangles.
Triangles that have sides that are all different lengths are called scalene triangles.
Triangles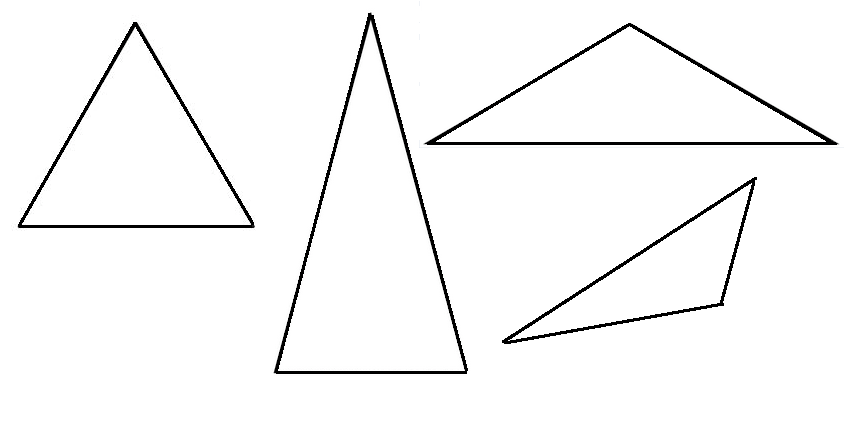
Top tip! If a triangle has sides that are all the same length it will look exactly the same if you rotate or turn it once, but a triangle with sides that are different lengths won't.
Teacher notes
Although students don't need to learn the names of the different types of triangles, it is useful for them to understand that triangles are not all the same. You could ask them to point out the different types of triangles on the drawing.
Use a template of an equilateral triangle to demonstrate that when it is rotated 90 degrees it looks the same.
Did you know?
A triangle is the strongest of all the shapes. Objects and buildings that need to be strong, often have triangles in their structure.
- Can you spot the triangles in these bridges?
- Can you spot the triangles in the frame of this (extremely long) bicycle? (A bicycle made for five people would have to be very very strong!)
- Look out for triangles in buildings and bicycles when you next go for walk...
Pentagons, hexagons and octagons
Can you see some shapes with lots of sides and lots of corners?
Can you work out what they are?
Here are some clues...
- A pentagon has 5 sides and 5 corners – can you find a pentagon?
- A hexagon has 6 sides and 6 corners – can you find a hexagon?
- An octagon has 8 sides and 8 corners – can you find an octagon?
Did you know?
The black and white pattern on a football is made from pentagons and hexagons.
Look at this sculpture of a football.
- What colour are the hexagons?
- What colour are the pentagons
Top tip! Count the sides of the shapes to find out what they are.
The honeycombs where bees store their honey are made from lots of hexagon-shaped cells.
Western honey bee on a honeycomb
You might spot an octagon on your way home from school...!
Stop sign
Circles
Circles are all around us.
- Try drawing a circle in the air with your finger.
- Can you see any circles in this painting of a market stall?
- How are circles different from all the other shapes we have looked at so far?
- How many corners does a circle have?
- How many sides does it have?
About circles
All the shapes we have looked at so far have straight lines, but circles are made from a curved line and have no corners.
They also only have one side. All the other shapes we have looked at have 3 or more sides.
Semi-circles
If you cut a circle in half, you get a very different shape called a semi-circle.
This sculpture was made by an artist called Barbara Hepworth. It is made of two semi-circles with circles inside the semi-circles. (Barbara Hepworth often added circles to her sculptures.)
- Can you spot the semi-circles?
- How is a semi-circle different from a circle?
- How many sides and corners does it have?
- Is it made from curved or straight lines?
About semi-circles
A semi-circle is half a circle. It is different from a circle because it has 2 sides – a straight side and a curved side. It also has 2 corners, while a circle has no corners.
Circles and semi-circles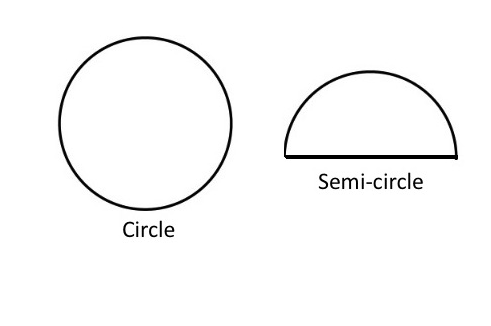
2D shapes and symmetry
If you draw a line down the centre of a circle, the two halves are exactly the same.
Shapes that have two identical halves are symmetrical shapes.
Have a look at these 2D shapes. Imagine drawing a line down the centre of them from the top to the bottom.
- Would each half look exactly the same?
2D shapes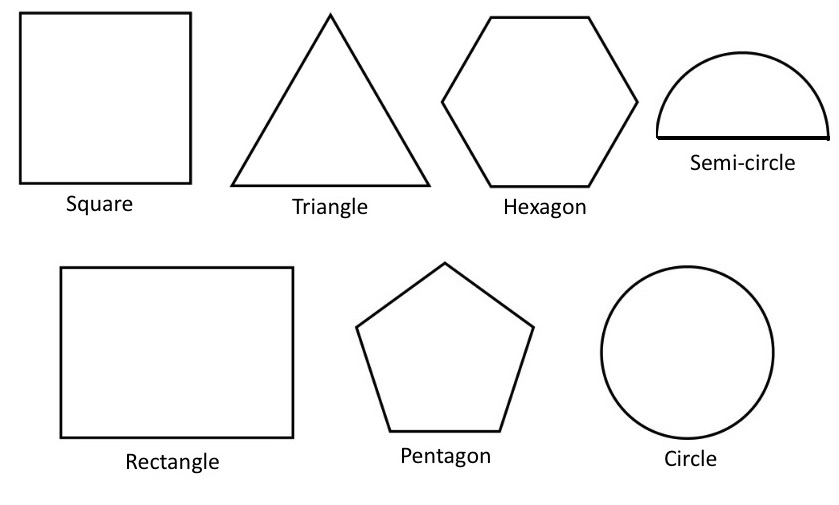
All of these shapes have a vertical line of symmetry. (A vertical line is a straight line that goes up and down.)
Now imagine drawing a line through the middle of each shape from side to side. (A line that goes from side to side is called a horizontal line.)
- Would each half look exactly the same?
- Are there any shapes that would have different shaped halves?
Teacher notes
It may be helpful to fold paper shape templates in half to illustrate the vertical and horizontal lines of symmetry.
For more advanced students you could also introduce the idea of multiple lines of symmetry.
- A square has four lines of symmetry.
- An equilateral triangle has three lines of symmetry.
- A circle has infinite lines of symmetry.
Activity: I spy 2D shapes challenge
As a class, look through the artworks in the slideshow below and ask your students to find 2D shapes.
You could approach the challenge as an 'I spy' game.
- Ask individual students in the class to choose a shape they can see and tell the class the letter that the shape name starts with ('I spy with my little eye a shape beginning with [letter]')
- The rest of the class should then try and spot the shape in the picture and describe what its properties are.
Junction of Bootham and Gillygate 1990
unknown artist
Two Teas and a Plate of Sandwiches 1998
Sue Adsett (b.1970)
Tower Block Dweller 1998
Jiro Osuga (b.1968)
Mrs Thomas Howard and the Kondor, 1940 2005
Stephen Chaplin (b.1934)
Cumbrian Village Bowling Team and Supporters Playing Away and Waiting for the Coach late 1960s
Peter Brook (1927–2009)
Bologna 1979
Anthony Moore
George Formby: Speed Ace 1989
Frances Broomfield (b.1951)
Knowing 1996
Michael Craig-Martin (b.1941)
© Michael Craig-Martin. Courtesy Gagosian Gallery. Image credit: Manchester Art Gallery
Activity: 2D shape classroom scavenger hunt
Task your students to work in pairs or small groups and find shapes around the classroom. Students could either:
- collect shapes (such as a rectangular piece of paper)
- draw around shapes they find or see (such as a hexagonal pencil end)
- or draw a picture of the shape and make a note of where they saw it (such as a square window).
In advance of the lesson, you may want to make sure that there are examples of shapes around the classroom and supplement them with extra objects that include shapes as necessary!
Set a time limit of 5 minutes.
Art & design activity suggestions
Before the lesson
Prepare shape templates for students to draw around (squares, rectangles, circles, triangles, etc.).
Shape templates
You could either make card templates or collect objects such as bottle tops or jar lids, tin cans, dominoes, etc. – anything that has a circular, square or rectangular face. (Objects with triangular, hexagonal, octagonal and pentagonal faces may be harder to find so you may need to make these templates!)
Make an abstract picture or pattern from 2D shapes
In this resource, we have looked at lots of paintings, prints and drawings. Many of these are abstract artworks made from geometric shapes.
Task your students with making an abstract picture or pattern using the shape templates.
- They could overlap the shapes (as artist Pamela Ward has done with her Interwoven Triangles) and then paint or colour in the new shapes that have been made by the overlaps.
(For more detailed activity instructions, see the Art UK activity: Make a 2D artwork from abstract shapes.)
- They could arrange and repeat shapes across the page, combining one or two shapes to make a pattern. Encourage them to think about the order or sequence of their arrangement.
- Or they could explore shapes that fit together or tesselate, to form a pattern. (Find out more about tesselation in this BBC Bitesize guide.)
Be inspired by more abstract pictures and patterns made using shapes, on Art UK:
Sekela Khuluma 1980
Terry Edmond (1947–2020)
6231 1962
Simon Nicholson (1934–1990)
Painting/Maquette No 2 (Mixed Media) 1960s
Malcolm Edward Hughes (1920–1997)
1940–43 (two forms) 1940–1943
Ben Nicholson (1894–1982)
Composition with Number Six 1966
Anwar Jalal Shemza (1928–1985)
Two Complementaries – Study 1970
Wilhelmina Barns-Graham (1912–2004)
Rectangles 2004
R. Jarrett
Grey Grid 1978
Sydney Harry (1912–1991)
Make a 2D shape robot
Artist Ithell Colquhoun has used simple shapes to create a robot-like football player (with a football on its head and goalposts at its feet).
Using shape templates, task your students with making a simple robot picture using shapes. (It could be a humanoid or animal-shaped robot.)
- It might be easiest for students to use shape templates or objects and draw around them.
- They could colour or paint the shapes or cut the shapes out of coloured paper and make a robot collage.
- Encourage students to think about which shapes could be used to make the different parts of the robot (the legs, the body, the head, etc.) and how they can join shapes together.
Ithell Colquhoun was associated with the Surrealist movement, so encourage your students to be as surreal as they like with their shape robots!
For more detailed activity instructions (and more 2D shape robot ideas) take a look at the Art UK activity: Make a robot from 2D shapes.
Stories
-
Art UK Home School: make a dazzle sculpture with Lisa Traxler 17 June 2020, Selina Levinson Drake -
Remembering the sculptor Phillip King 27 August 2021, Chris Mugan -
Terry Frost: a sense of delight in abstraction 14 March 2019, Jo Baring -
Bridget Riley: top of the Ops 24 April 2018, Andrew Greg -
Josef Albers' 'Homage to the Square: R-NW IV' 11 March 2016, Humphrey Ocean -
Spots and stripes: the modernist works of Ben Nicholson 15 June 2020, Caroline Maclean
Downloads
Download Art UK Investigate 2D shapes
More Abstraction resources
-
ActivityMake a robot from 2D shapes-
KS1 (ENG)KS2 (ENG)KS1 (NI)KS2 (NI)CfE L1 (SCO)CfE L2 (SCO)PS2 (WAL)PS3 (WAL)
-
-
Lesson planPrunella Clough: from source materials to abstract paintings-
KS3 (ENG)KS3 (NI)CfE L4 (SCO)KS3 (WAL)
-
More Art resources
-
ActivityMake your own pet from junk-
KS1 (ENG)KS2 (ENG)KS1 (NI)KS2 (NI)CfE L1 (SCO)CfE L2 (SCO)PS2 (WAL)PS3 (WAL)
-
-
ActivityMake a colour sculpture and tell a story!-
KS1 (ENG)KS2 (ENG)KS1 (NI)KS2 (NI)CfE L1 (SCO)CfE L2 (SCO)PS2 (WAL)PS3 (WAL)
-
-
Lesson planThe Superpower of Looking Kit-
KS2 (ENG)KS2 (NI)CfE L2 (SCO)PS3 (WAL)
-